Max Planck - Quantenpostulat

Als Max Planck im Jahre 1895 die Quantisierung der sog. "Schwarzkörperstrahlung" postulierte und damit die Schwächen des Wienschen Strahlungsgesetzes und des Rayleigh-Jeans befreite, hatte die Thermodynamik mit ihren Hauptsätzen und schon mindestens 100 erfolgreiche Jahre hinter sich. Da Planck, ab 1889 ja Professor an der  Friedrich-Wilhelms-Universität in Berlin, Vorlesungen auch über Thermodynamik hielt, war ihm die Proportionaltätskonste k - die sog. Boltzmann-Konstante - als Umrechnungsfaktor zwischen Temperatur und Energie in der statistischen Thermodynamik sicher bekannt. 
Vielleicht lag es ihm bei seinen Forschungen nahe, für die Umrechnung einer Wellenfrequenz f in eine Energie auch eine Hilfsgröße h zu postulieren: E = h*f:

1894 beginnt der Planck mit den Forschungen über Wärmestrahlung und entdeckt 1899 die Naturkonstante h - bald plancksches Wirkungsquantum genannt. 1900 entwickelte Max Planck ein Gesetz, dass die Ausstrahlung elektromagnetischer Energie durch einen schwarzen Körper beschreibt, das "plancksche Strahlungsgesetz".

Die heute als Plancksches Wirkungsquantum bekannte Größe hat als Naturkonstante den Wert 6,626⋅10^-34 Js.

Jegliche Strahlungsenergie kann nur in Vielfachen dieses Wert erfolgen.

Das plancksche Strahlungsgesetz:

In diesem Beitrag zum Projekt "100 Jahre Quantenphysik" sollen nun Details der Planckschen Untersuchungen einige Zugänge und Anwendungen dargestellt werden:

Hohlraumstrahlung, schwarzer Körper Besonders Der Begriff des "schwarzen Körpers" ist ein wenig irreführend, meint er doch nicht die Farbe des Gegenstands, sondern dass er alle einfallende Strahlung komplett absorbiert. Beispiele sind natürlich ein völlig 'schwarzer' Körper mit einer Bohrung, aber auch die Sonne oder sogar das Universum! Untersucht wird die 'Farbe', besser Energie der Strahlung, welcher Körper in Abhängigkeit von seiner Temperatur aussendet.

Strahlungsgesetze

Messung	Rayleigh-Jeans	Wien	Planck
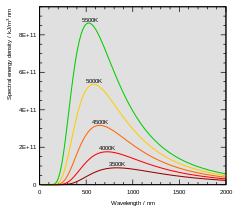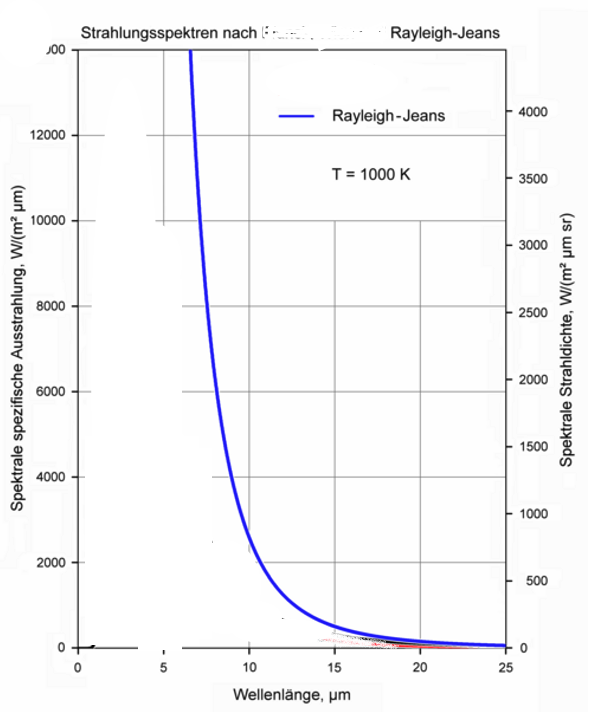	zu hohe Werte im kurzwelligen Bereich: UV-Kathastrophe	zu niedrige Werte im langwelligen Bereich

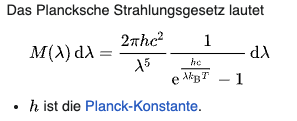• ein formaler Zugang zur Überwindung der Schwächen von Rayleigh-Jeans und Wien:
  
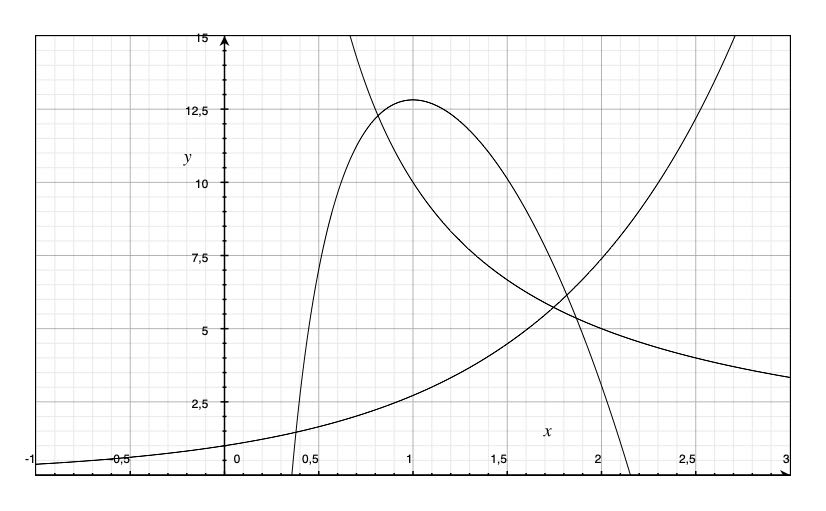
  Diese Graphik wurde mit dem GRAPHER des MAC erstellt. Der "Buckel" entsteht durch Multiplikation von zwei modifizierten Potenz- bzw. Exponentialfunktionen
• Anwendungsbeispiele
  • Temperatur der Sonnenoberfläche, max. Farbe der Sonne grün-gelb λ = 600 nm
    
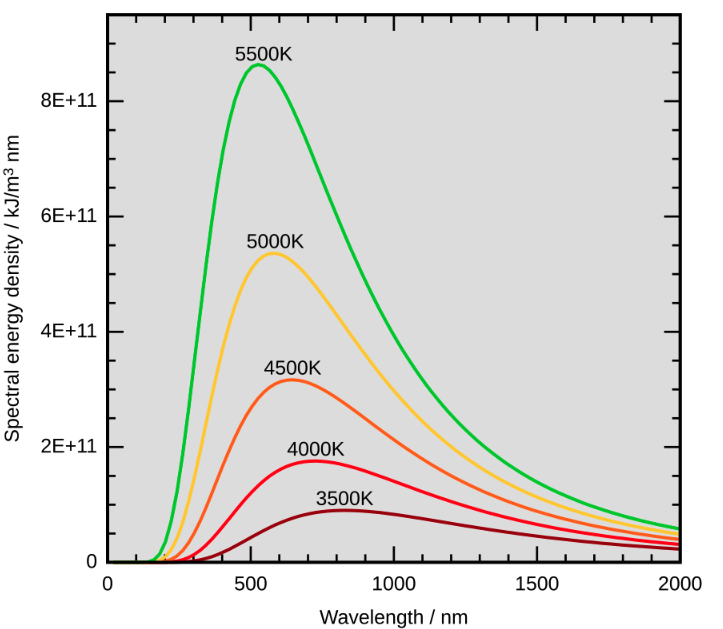
    Effizienz von Glühbirnen, LED-Leuchten: ....